Logic Composition

Within these castle walls be forged Mavens of Computer Science ...

— Merlin, The Coder

Curriculum

Coder Merlin™  Computer Science Curriculum Data

Unit: Boolean algebra Experience Name: Logic Composition (W1016) Next Experience: () Knowledge and skills: §10.327 Demonstrate understanding and proficiency in the use of logic composition Topic areas: Boolean algebra Classroom time (average): 40 minutes Study time (average): 180 minutes Successful completion requires knowledge: understand the use of logic composition to build complex Boolean operations from simpler building blocks Successful completion requires skills: demonstrate proficiency in using logic composition to build complex Boolean operations from simpler building blocks

Introduction

Logic gates can be composed in the same way that Boolean functions can be composed, allowing the construction of a physical model of all of Boolean logic. Combining multiple gates enables us to build complex functionality from simpler building blocks.

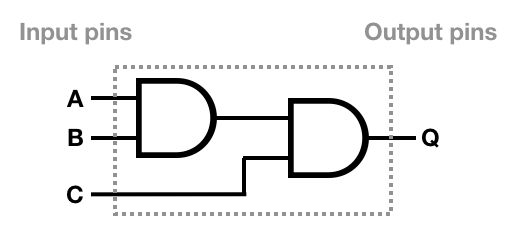
Three-Input And Gate

Three Input AND Gate

Consider this three input AND gate internally constructed of two, two-input AND gates. Logically, this gate has three inputs and one output, regardless of how the gate is constructed internally. The truth table for this composition is:

Inputs			Outputs
$A$	$B$	$C$	$Q=A\land B\land C$
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	1

Helpful Hint

Take the time to recreate this table (and those that follow) on your own

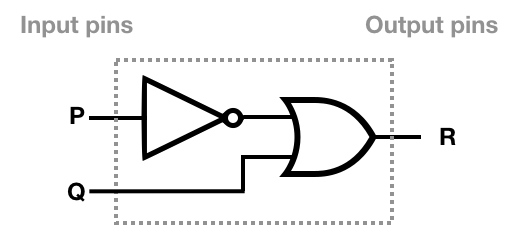
Implication Gate

IMPLY gate

Consider this IMPLY gate internally constructed of a NOT gate and an OR gate. Logically, this gate has two inputs and one output, regardless of how the gate is constructed internally. The truth table for this composition is:

Inputs		Outputs
$P$	$Q$	$Y=\neg A\lor B$
0	0	1
0	1	1
1	0	0
1	1	1

Implication is formally indicated by a forward arrow, i.e. $p\rightarrow q$, meaning, if p is true, then q is also true. As an example, consider the implication, "if it's raining then I'll carry my umbrella". There are four cases, only one of which yields false:

Raining	Equipped with Umbrella	Evaluation of Statement	Explanation
No	No	true	It's not raining, so it doesn't matter if I'm carrying an umbrella or not.
No	Yes	true	It's not raining, so it doesn't matter if I'm carrying an umbrella or not.
Yes	No	false	It is raining, and I am not carrying an umbrella. This contradicts the implication.
Yes	Yes	true	It is raining, and I am carrying my umbrella.

First Steps

This exercise relies on an external website which will enable you to easily experiment with logic gates and form various compositions with the components. The links on this wiki page will preload the relevant gates currently under discussion. For best results, open the links in a separate window so that you can continue to read the wiki while you experiment.

• The "L" indicates a Low voltage which usually represents zero or false
• The "H" indicates a High voltage which usually represents one or true
• The layout flows from left to right.
• Inputs will be leftmost and output will be rightmost.
• Clicking on an input will toggle the input from Low to High or from High to Low
• When an input is changed, the result will instantly impact the rest of the digram.

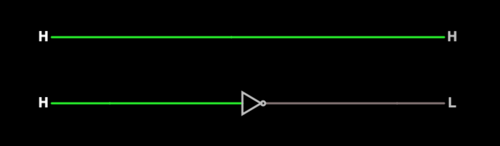
Input, Output, and an Inverter

Click on the image ("Wire and Inverter") and open the link in a different window, then return to the wiki:

Wire and Inverter

1. Click on the leftmost (input) H in the top diagram which simply represents a wire.
   1. What happens to the H?
   2. Does the color of the wire change?
   3. How is the output impacted?
2. Click on the leftmost (input) H in the bottom diagram which represents an inverter.
   1. What happens to the H?
   2. Does the color of the wire change?
   3. How is the output impacted?

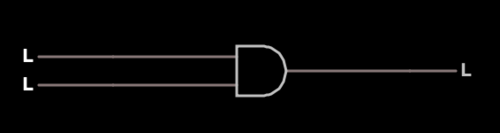
AND Gate

Click on the image ("AND Gate") and open the link in a different window, then return to the wiki:

AND Gate

1. Click on the top L input.
   1. What happens to the top L?
   2. What happens to the output?
2. Click on the bottom L input.
   1. What happens to the bottom L?
   2. What happens to the output?
3. Click several more times on the inputs until you're able to consistently predict the output.

Circuit Editor Basics

Starting Over

1. To begin a new circuit, select Circuit | Blank Circuit from the menu bar.

Inserting a Logic Gate

1. To insert a new logic gate, select Draw | Logic Gates, Input, and Output from the menu bar.
2. Select the specific gate that you'd like to add. Your choices are:
   • Inverter
   • NAND
   • NOR
   • AND
   • OR
   • XOR
3. Click with the mouse (but don't let go) and drag the cursor in the direction you'd like the gate to go
4. Release the mouse

You can repeat the last two steps to draw the same gate again and again without needing to return to the menu.

Moving Objects

1. Press the SPACE key to enter drag mode. You'll then be able to drag objects. Object with connection points which are sufficiently close to one another will be connected.

Logic Input

Logic inputs can be used to specify the input for a gate. Clicking on the "L" or "H" of an input will toggle its state.

1. Select Draw | Logic Gates, Input and Output | Add Logic Input
2. Click with the mouse (but don't let go) and drag the cursor in the direction you'd like the input to go
3. Release the mouse

Logic Output

Logic outputs can be used to display the output of a gate. Clicking on the "L" or "H" of an output will do nothing.

1. Select Draw | Logic Gates, Input and Output | Add Logic Output
2. Click with the mouse (but don't let go) and drag the cursor in the direction you'd like the output to go
3. Release the mouse

Wire

Wires can be used to connect inputs together.

1. Select Draw | Add Wire
2. Click with the mouse (but don't let go) and drag the cursor in the direction you'd like the wire to go
3. Release the mouse

Text

Text can be used to add labels.

1. Select Draw | Outputs and Labels | Add Text
2. Click with the mouse (but don't let go) and drag the cursor in the direction you'd like the text to go
3. Release the mouse

Take some time now to play with the editor and continue until you feel comfortable.

Exercise Preparation

1. Construct a three-input AND gate
2. Construct an IMPLY gate

Exercises

Helpful Hint

• Refer to DeMorgan's Law in W1013 Boolean Algebra
• Refer to The Special Role of NAND and NOR Gates W1014 Logic Gates

Exercises

• For ALL of these exercises, you may use ONLY:
  • Wires
  • Logic Inputs
  • Logic Outputs
  • Two-input NAND Gates
• Construct your work using Falstad's Editor
• All circuits must be on a single page
• Label the page (using Text) with:
  • Your name
  • The date
• Begin each circuit with a Blank Circuit
• Label each circuit diagram (using Text) with:
  • The name of the logic gate (e.g. "NOT")
• Save the document using the Save As... option from the File submenu and then click on the link presented
• The file contains your work for the exercise. Create a new subdirectory, J1016, in your Journals directory. Upload the file to the J1016 directory via SFTP. Be sure to push the file to your GitHub repository.

---

1. Construct a NOT gate
2. Construct an AND gate
3. Construct an OR gate
4. Construct an XOR gate
5. Construct a NOR gate

Excursions

Excursions

Seven-Segment LED

Consider a 7-segment LED display, as shown. The display is capable of indicating all decimal digits, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 and the hexadecimal digits a, b, c, d, e, and f.

• Constraining your output to a seven-segment display, draw each digit using only the segments provided.
• Consider a four-bit binary input, representing hexadecimal digits 0-f. Develop a series of logic gates which convert the four-bit input into a seven-segment output, such that the binary number on the four-digit input is correctly represented on the seven-segment display.
• Save a link to your engineering design in your journal.

Experience Metadata

Edit Experience Metadata

Experience ID	W1016
Next experience ID
Unit	Boolean algebra
Knowledge and skills	§10.327
Topic areas	Boolean algebra
Classroom time	40 minutes
Study time	3 hour180 minutes <br />
Acquired knowledge	understand the use of logic composition to build complex Boolean operations from simpler building blocks
Acquired skill	demonstrate proficiency in using logic composition to build complex Boolean operations from simpler building blocks
Additional categories