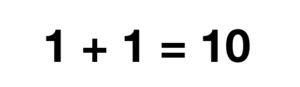Alternative Base Addition

Within these castle walls be forged Mavens of Computer Science ...

— Merlin, The Coder

1 + 1 = 10

Dark apple

Dark apple

Curriculum

Coder Merlin™  Computer Science Curriculum Data

Unit: Numbers Experience Name: Alternative Base Addition (W1012) Next Experience: () Knowledge and skills: §10.311 Demonstrate proficiency in the use of positional notation to represent and convert between numbers in the binary, octal, decimal, and hexadecimal systems §10.312 Demonstrate proficiency in counting in the binary, octal, decimal, and hexadecimal systems §10.313 Demonstrate proficiency in adding two operands specified in the binary, octal, decimal, and hexadecimal systems Topic areas: Positional notation Classroom time (average): 60 minutes Study time (average): 180 minutes Successful completion requires knowledge: understand positional notation; understand how numbers specified in positional notation are added Successful completion requires skills: ability to use positional notation to represent numbers in the binary, octal, decimal, and hexadecimal systems; ability to convert between representations of numbers in the binary, octal, decimal, and hexadecimal systems; ability to count by one using numbers in the binary, octal, decimal, and hexadecimal systems; ability to add together numbers in the binary, octal, decimal, and hexadecimal systems

Addition (Decimal System)

Addition is a basic (and critical) operation. Important properties of addition include:

• Addition is commutative, meaning that the order of the operands does not matter
  • $a+b=b+a$
• Addition is associative, meaning that when we're adding more than two operands, the order that we perform the addition does not matter
  • $(a+b)+c=a+(b+c)$
• The identity element for addition, also termed the additive identity, is zero
  • $a+0=a$
• The operator for addition is the plus ($+$) sign
• The operands for addition are called addends

Let's review how we perform addition in the number system with which we are most familiar, the decimal system.

There are a few simple rules when adding non-negative, whole numbers:

1. Align the addends vertically, flush right. (This step ensures that the position multiplier is the same for both addends in each column.)
2. If any addend has fewer digits than the addend with the maximum digits, we may place a zero in columns to the left of the existing addend. (Leading zeroes don't affect the value.)
3. Starting from the right-most column, add the two digits of the addend and the carry. Note that this means that we are adding three operands in each column. If the sum exceeds the quantity that can be represented with a single digit, carry a one to the column to the left.
4. Repeat the process with the column to the left until reaching the final column.

Let's look at a few examples:

$3_{10}+5_{10}$

To add $3_{10}+5_{10}$ we: Align the digits vertically Add the right-most (and only) column, containing a 3 and a 5, yielding 8. Because this is less than the quantity that can be represented by a single digit, we have no carry. Done

carry 0 0 addend 0 3 addend 0 5 sum 0 8

$3_{10}+8_{10}$

To add $3_{10}+8_{10}$ we: Align the digits vertically Add the right-most column, containing a 3 and an 8, yielding 11. Because this is greater than the quantity that can be represented by a single digit, we carry. We move to the left, where the next column contains only a lone value, the carry. We sum this with the addend digits in the same column, yielding 1. Done

carry 1 0 addend 0 3 addend 0 8 sum 1 1

$104_{10}+397_{10}$

To add $104_{10}+397_{10}$ we: Align the digits vertically Add the right-most column, containing 4 and 7, yielding 11. Because this is greater than the quantity that can be represented by a single digit, we carry. We move to the left, where the next column contains the carry and a 9, yielding 10. Because this is greater than the quantity that can be represented by a single digit, we carry. We move to the left, where the next column contains the carry, a 1, and a 3, yielding 5. Because this is less than the quantity that can be represented by a single digit, we have no carry. Done

carry 1 1 0 addend 1 0 4 addend 3 9 7 sum 5 0 1

Observe

Observe, Ponder, and Journal: Section 1

1. Describe the general process for executing addition, regardless of base.

Addition (Octal System)

There's no need for any additional rules for the octal system. In fact, for all systems, the rules are exactly the same! But let's review the octal number line before proceeding to an example:

How would we add $7_{8}+4_{8}$?

Caution

Be sure that you fully understand the above diagram before proceeding.

$104_{8}+367_{8}$

To add $104_{8}+367_{8}$ we: Align the digits vertically Add the right-most column, containing 4 and 7, yielding 13. Because this is greater than the quantity that can be represented by a single digit, we carry. We move to the left, where the next column contains the carry and a 6, yielding 7. Because this is less than the quantity that can be represented by a single digit, we have no carry. We move to the left, where the next column contains a 1, and a 3, yielding 4. Because this is less than the quantity that can be represented by a single digit, we have no carry. Done

carry 0 1 0 addend 1 0 4 addend 3 6 7 sum 4 7 3

Observe

Observe, Ponder, and Journal: Section 2

1. What special factors need to be considered when executing addition with octal numbers?

Addition (Hexadecimal System)

Let's review the hexadecimal number line before proceeding to an example. How would we add $9_{16}+7_{16}$?

Remember that in number systems with bases greater than 10, by convention, we use letters in place of digits.

Digit	Value
A	10
B	11
C	12
D	13
E	14
F	15

$7A9_{16}+6B7_{16}$

To add $7A9_{16}+6B7_{16}$ we: Align the digits vertically Add the right-most column, containing 9 and 7, yielding 10. Because this is greater than the quantity that can be represented by a single digit, we carry. We move to the left, where the next column contains the carry and an A and B, yielding 16. Because this is greater than the quantity that can be represented by a single digit, we carry. We move to the left, where the next column contains the carry, a 7, and a 6, yielding 14 (represented by "E"). Because this is less than the quantity that can be represented by a single digit, we have no carry. Done

carry 1 1 0 addend 7 A 9 addend 6 B 7 sum E 6 0

Observe

Observe, Ponder, and Journal: Section 3

1. What special factors need to be considered when executing addition with hexadecimal numbers?

Addition (Binary System)

Let's jump right in to an example:

$0011\;\;1010_{2}+0001\;\;0111_{2}$

To add $0011\;\;1010_{2}+0001\;\;0111_{2}$ we: Align the digits vertically Add the right-most column, containing 0 and 1, yielding 1. Because this is less than the quantity that can be represented by a single digit, we have no carry. We move to the left, position 1, where we have no carry, a 1 and a 1, yielding 10. Because this is greater than the quantity that can be represented by a single digit, we carry. We move to the left, position 2, where we have a carry, a 0 and a 1, yielding 10. Because this is greater than the quantity that can be represented by a single digit, we carry. We move to the left, position 3, where we have a carry, a 1 and a 0, yielding 10. Because this is greater than the quantity that can be represented by a single digit, we carry. We move to the left, position 4, where we have a carry, a 1 and a 1, yielding 11. Because this is greater than the quantity that can be represented by a single digit, we carry. We move to the left, position 5, where we have a carry, a 1 and a 0, yielding 10. Because this is greater than the quantity that can be represented by a single digit, we carry. We move to the left, position 6, where we have a carry, a 0 and a 0, yielding 1. Because this is less than the quantity that can be represented by a single digit, we have no carry. We move to the left to the final column, where we have no carry, a 0 and a 0, yielding 0. Because this is less than the quantity that can be represented by a single digit, we have no carry. Done

position 7 6 5 4 3 2 1 0 carry 0 1 1 1 1 1 0 0 addend 0 0 1 1 1 0 1 0 addend 0 0 0 1 0 1 1 1 sum 0 1 0 1 0 0 0 1

Observe

Observe, Ponder, and Journal: Section 4

1. What special factors need to be considered when executing addition with binary numbers?

Key Concepts

Key Concepts

• Addition is a basic (and critical) operation
• Addition is commutative
• Addition is associative
• The identity element for addition, also termed the additive identity, is zero
• The operator for addition is the "+" sign
• The operands for addition are called addends
• When adding non-negative, whole numbers:
  • Align the addends vertically, flush right
  • If any addend has fewer digits than the addend with the maximum digits, we may place a zero in columns to the left of the existing addend
  • Starting from the right-most column, add the two digits of the addend and the carry. If the sum exceeds the quantity that can be represented with a single digit, carry a one to the column to the left.
  • Repeat the process with the column to the left until reaching the final column

Exercises

Exercises

•  J1012  Create a journal and answer all questions in this experience. Be sure to:
  • edit your journal using emacs within your ~/Journals directory
  • properly name your journal as J1012.txt
  • include all sections of the journal, properly formatted
  • push your changes to GitHub
  • properly tag your journal as J1012.Final
  • push your tag to GitHub
•  M1012-10  Complete  Merlin Mission Manager  Mission M1012-10.

References

• Addition (Wikipedia)

Experience Metadata

Edit Experience Metadata

Experience ID	W1012
Next experience ID
Unit	Numbers
Knowledge and skills	§10.311 §10.312 §10.313
Topic areas	Positional notation
Classroom time	60 minutes
Study time	3 hours180 minutes <br />
Acquired knowledge	understand positional notation understand how numbers specified in positional notation are added
Acquired skill	ability to use positional notation to represent numbers in the binary, octal, decimal, and hexadecimal systems ability to convert between representations of numbers in the binary, octal, decimal, and hexadecimal systems ability to count by one using numbers in the binary, octal, decimal, and hexadecimal systems ability to add together numbers in the binary, octal, decimal, and hexadecimal systems
Additional categories